Experimentos

Cómo ya se mencionó, el primer paso fue extraer capturas de los videos por medio de una función de cv2. Posteriormente se eligieron imágenes representativas para continuar trabajando con ellas.

El paso posterior fue la identificación de objetos, por lo que a partir de aquí se detallan los pasos realizados para cada método.

Método 1

A continuación, se muestran los resultados del procesamiento de una imagen aleatoria del dataset, es decir, se muestran los resultados de la binarización adaptativa, aplicación de operaciones morfológicas y etiquetado:

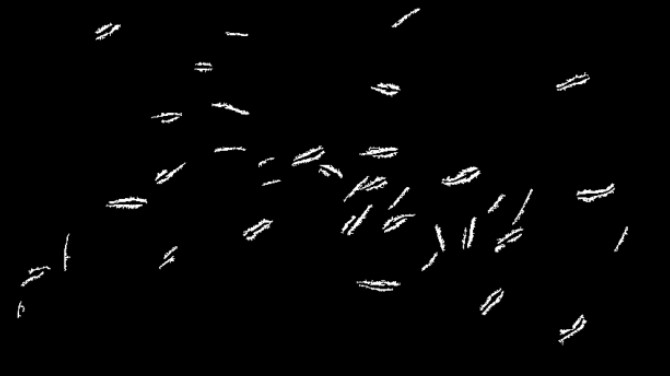
Como se puede ver, se llega a un resultado bastante satisfactorio donde se logra identificar como objetos únicamente los peces.

El paso siguiente fue encapsular estos pasos en una función y aplicar dicha función a varias imágenes. Al hacer esto, se constata que para muchas imágenes el resultado de este pre-procesamiento no es tan satisfactorio. El principal problema del pre-procesamiento es que el método detecta muchos objetos que no son peces, y esto sucede en mayor ante condiciones desfavorables para la toma de las fotos (viento (que genera olas en el agua) e iluminación no uniforme debido a la posición del sol (que en algunos casos satura completamente algunas partes de la imagen). A continuación se muestra el resultado final de dicha función para un par de imágenes en el que este procesamiento arroja resultados bastante malos:

Para solucionar esto, se procedió a entrenar un modelo que pueda diferenciar los objetos entre peces y no peces. Para esto, se construyó un primer modelo auxiliar, en base a 40 objetos (20 de ellos peces, 20 no peces) con el cual se pre-etiquetaría todo el modelo, para luego corregir las etiquetas que estaban mal de forma manual. A continuación, se muestra el análisis de pares de dispersión, donde se visualiza que tan bueno es cada par de variables para la separación de los objetos entre Peces y “No peces”.

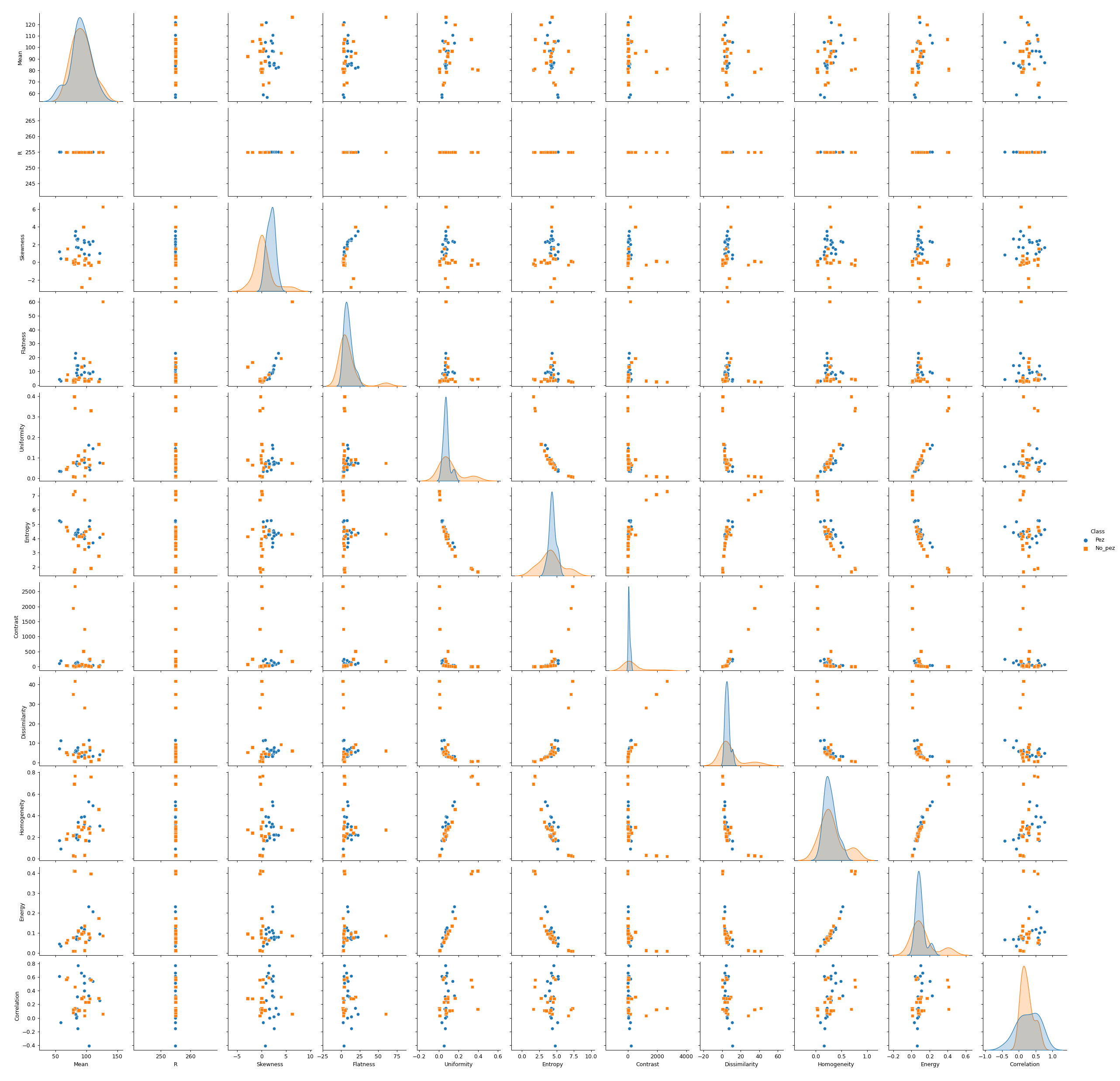
Las variables consideradas en este análisis para el modelo auxiliar son únicamente descriptores del histograma o descriptores de la matriz de coocurrencia. Las variables elegidas para usar en el modelo auxiliar son “Correlation” y “Skewness”. Con estas se entrena un modelo KNN con K=2. Posteriormente, se etiquetan todos los objetos detectados en el dataset. Este modelo auxiliar es el mismo para ambos métodos.

Posteriormente, se procedió a corregir las etiquetas manualmente. Se corrigieron únicamente las primeras 500 etiquetas (de un total de 6000), por lo que el modelo se entrenó con 300 objetos, se testearon diferentes modelos con 200 objetos. Para el método 2 se lleva un procedimiento diferente.

Se repite el análisis de dispersión para pares de variables, para entender con qué variables alimentar al modelo principal: a partir del análisis visual de este gráfico se desprende que las variables Correlation, Dissimilarity, Skewness y área son buenas variables para considerar en el modelo.

Para este método, únicamente se evaluaron modelos utilizando KNN con distintas combinaciones de variables y distinto K.

El mejor modelo que se encontró fue el generado utilizando las variables:

      Correlation

      Skewness

      A/perímetro

Este obtuvo una exactitud total de 94%, sin embargo, cuando analizamos la matriz de confusión y métricas tales como la precisión del modelo para la clase Pez encontramos un efecto no deseado:

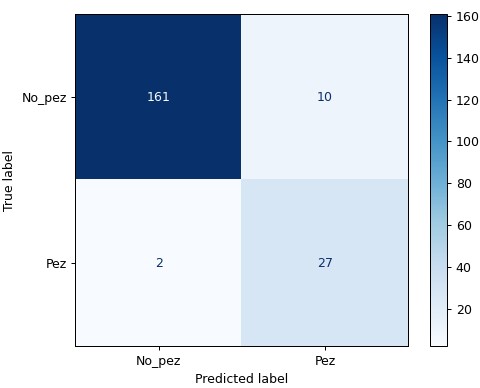
Como se puede ver, el modelo tiene una muy buena performance global, llegando a una exactitud de 94%. Sin embargo, considerando la finalidad de este modelo, que es el conteo de peces para determinar la cota máxima de pesca buscando la conservación de la especie, vemos que este modelo presenta un grave problema. Y el gran problema que tiene es que sobredimensiona (+27%) la cantidad de peces:

Número real de peces: 29

Número de peces detectados: 37

Este problema puede deberse a que el método de pre-procesamiento se detecta una gran cantidad de objetos que no son peces, esto termina dificultando al modelo de clasificación. Por lo tanto, es esperable que con el método 2 se obtengan mejores resultados (la imagen resultante de la binarización es mucho más limpia, detecta los bordes mejor sin generar tanto ruido, por lo tanto detectará menos falsos objetos).

Por tener una desviación muy importante en el número de peces identificados, que es el principal parámetro que interesa conocer, se procede a analizar con mayor profundidad el método 2.

Método 2

A continuación, se muestra la imagen binarizada por este método y la imagen etiquetada y se las compara con las obtenidas por el método 1.

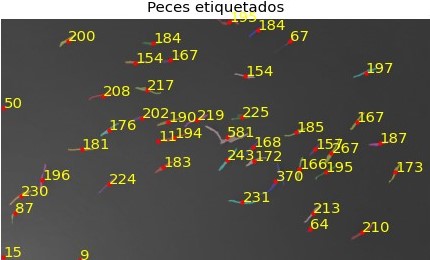
A simple vista, se ve que el método dos logra una imagen binarizada donde únicamente se detectan los objetos deseados, a diferencia del método 1. Si comparamos las imágenes etiquetadas…..

Posterioriormente se hizo el etiquetado de los primeros 700 objetos con el método 2 y se procedió a construir y evaluar distintos modelos. De los 700 objetos, se usan los primeros 300 para entrenar el modelo, luego se usan 237 para el testeo de los distintos modelos y se dajan 173 para la validación del mejor modelo obtenido (estas cantidades se hacen tras hacer una inspección visual de los grupos en cada subset para asegurar la máxima variabilidad de objetos en cada uno (y de condiciones en las que aparecen dichos objetos))

A partir de la gráfica de dispersión de pares de variables, se eligen posibles variables para construir modelos:

KNN

Para los siguientes modelos, se utilizan la combinación de variables con la que se obtuvo una mayor exactitud y Recall para la clase “Pez” en el mejor modelo construido usando KNN:

Correlation

Skewness

Perimetro

Este modelo con KNN = 4 obtiene los siguientes resultados:

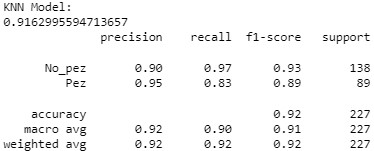
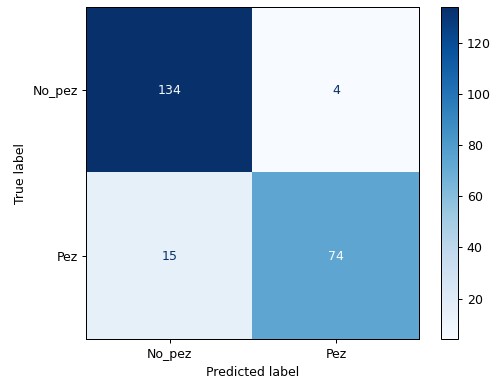
Como se puede ver, mejora notablemente la precisión respecto a la clase Pez y el modelo ya no cuenta peces de más, que por el objetivo del conteo es muy importante que sea de esta manera.

Se procedió a hacer un análisis con distintos K (distinto número de vecinos más cercanos a considerar en KNN):

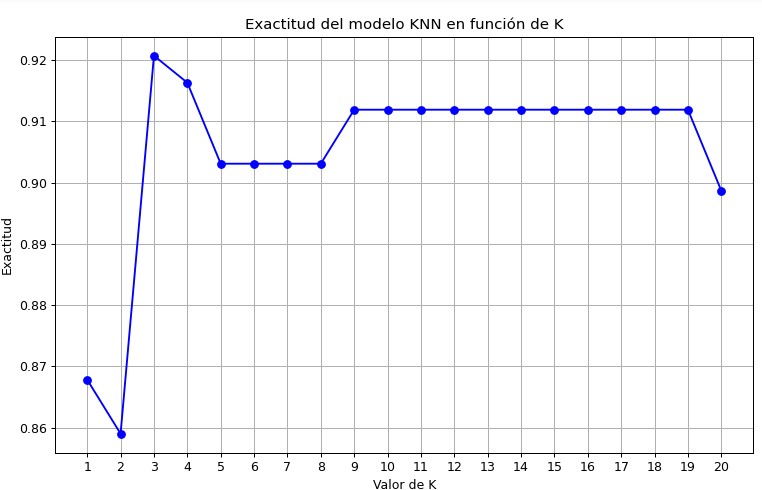
Cómo se puede ver, la mayor exactitud del modelo se obtiene con K=3, por lo que se procede a hacer la evaluación del modelo con dicho K. A continuación se muestran los resultados:

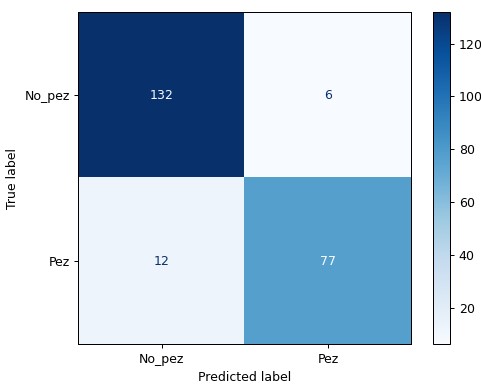
Por último, es de destacar la siguiente combinación de variables (con K=4, el modelo obtuvo una exactitud de 91.1%):

    Area

    Dissimilarity

SVM

Este modelo usa el algoritmo support vector machine. Como se mencionó anteriormente, el modelo utiliza las variables Correlation, Skewness y Perímetro y obtiene los siguientes resultados:

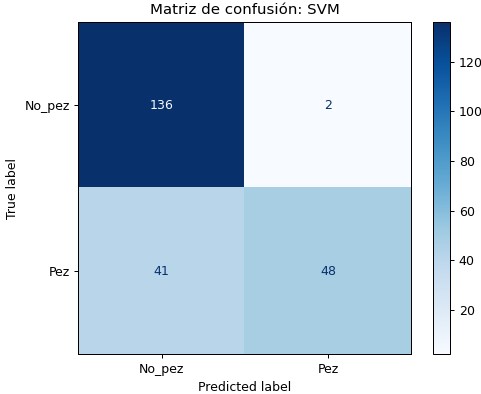
Árboles de decisión

DTC

El primer modelo utiliza el algoritmo decision tree clasifier. Como se mencionó anteriormente, el modelo utiliza las variables Correlation, Skewness y Perímetro y obtiene los siguientes resultados:

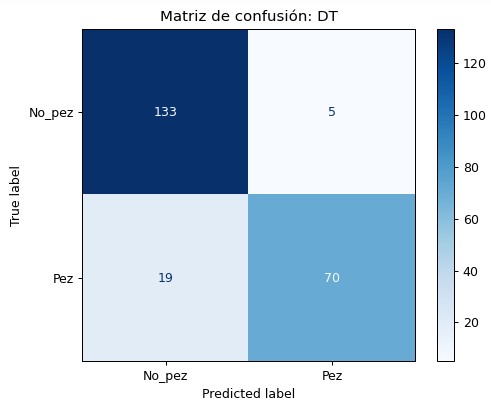
RF

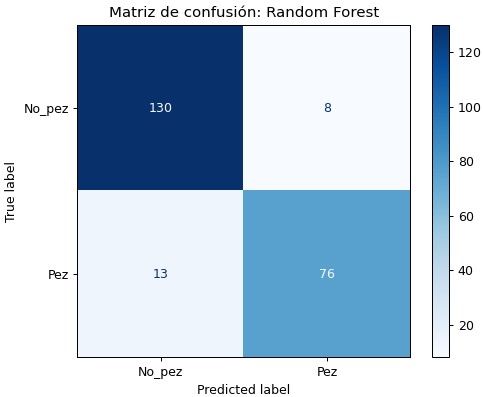
Este modelo utiliza el algoritmo random fortest, los resultados obtenidos son:

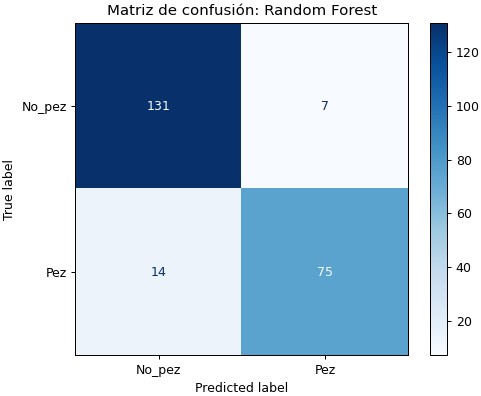
Para este algoritmo, se decide crear otro modelo usando las variables Area y Dissimilarity, que funcionaron particularmente bien para KNN. Esta es la matriz de confusión del modelo:

Cierre

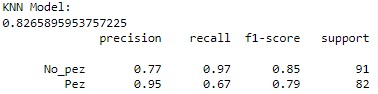
Se procede a evaluar el modelo KNN con K=3 (con las variables ) en el conjunto de validación. A continuación, se muestra exactitud, recall, matriz de confusión y otros parámetros:

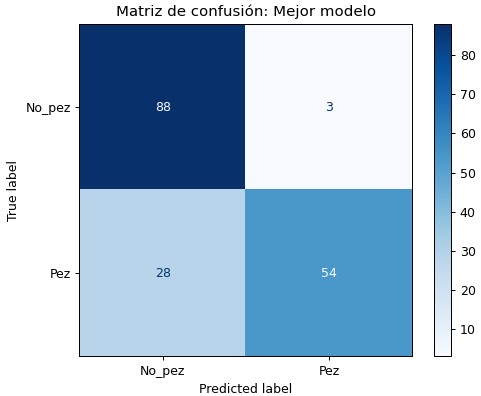
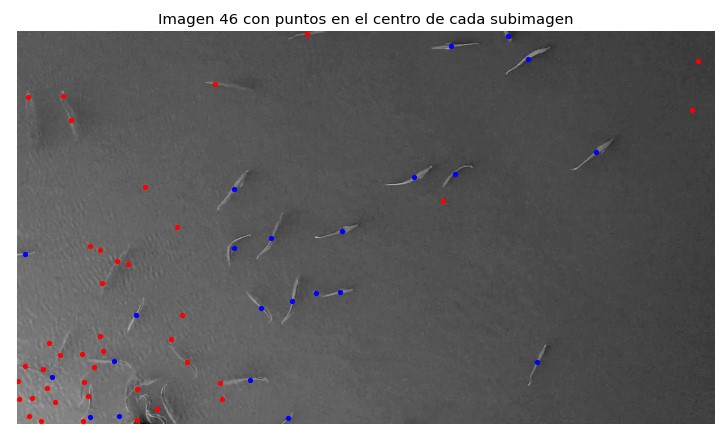
A continuación, se muestran 2 imágenes etiquetadas con este modelo, donde los puntos azules representan peces y los puntos rojos objetos que no son peces: